


Having this code also makes it possible to analyze the game a bit. This is also clear from the solver log: our MILP solver takes this into account automatically, and eliminates the symmetric solutions from the search tree. Thus we compare the solution values to 0.5 to decide if they are 0 or 1.įinally, it is obvious from the board that there are many symmetric solutions. So even if we restrict a variable to be either 0 or 1, values within of either value are still allowed. Here we need to be careful: when we are checking which variables are 1 (so that we know which move was taken) we cannot simply check for equality, because optimization solvers use a nonzero feasibility tolerance. When the solution is returned we want to print it using the original labelling. Then all we need to do is define the start and end positions and call the solver. Strengthening optimization problem formulations this way is the key to solving a lot of practical problems. This is not necessary, but it helps to solve the problem faster. We added an extra constraint on the number of pegs on the board after each move. In each round we can take exactly one move. A set of binary variables for each possible move in each round identifies which move was taken. It turns out that there are 40 possible moves: we store 20 of them in a data set, the other 20 are just the reverse moves. So we need to generate the possible differences between two consecutive rounds. At every move we change exactly three of these variables: two will go from 1 to 0, and one will go from 0 to 1. The position of the board is represented by 16 binary variables after each round: board = 1 if in round i a piece is placed in cell j, and 0 otherwise. There are a few points that I would like to elaborate on. The entire PROC OPTMODEL code with comments is at the end of this post. I thought to take the opportunity to solve this puzzle using SAS/OR optimization tools, in particular PROC OPTMODEL and the mixed integer linear programming (MILP) solver. The goal is to eliminate all but one peg, with the last peg ending up in the middle. You can jump over one peg, land on the immediately following cell, and remove the peg you jumped over.
#Peg solitaire solver u shape full#
The goal is the same: initially the board is full and only the middle cell is empty. That is why they tend to just collect dust.Ī friend of mine developed a different version, played on the following pentagonal board (see his blog post in Hungarian here): One difficulty with these games is that due to the large number of pegs it is very hard to think about a solution strategically from the beginning of the game. The goal in these games is to eliminate pegs by jumping over them with existing pegs until there is only one peg left, preferably in a predefined position.
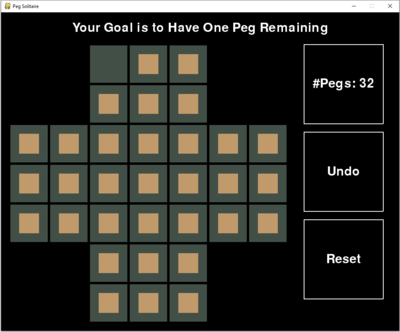
You probably have one in your game room or bought one for your kids at some point. I'm sure a lot of readers are familiar with the standard peg solitaire. I regularly use them at interviews: I ask the candidate either to solve a puzzle or to devise a (clever) mathematical algorithm that solves it. Bell, G.I love puzzles I have a few of them in my office. Difficult French positions, Search in Google Scholar Difficult English positions, Search in Google Scholar Symmetric Hexagon positions, Search in Google Scholar Symmetric 6圆 positions, Search in Google Scholar Symmetric French positions, Search in Google Scholar Symmetric English positions, Search in Google Scholar Peg Solitaire web site, Search in Google Scholar “Notes on solving and playing peg solitaire on a computer”, 2014. “On 33-hole solitaire positions with rotational symmetry”, 2012. “Solving triangular peg solitaire”, Journal of Integer Sequences, 11, 2008. “Triangular peg solitaire unlimited”, Games and Puzzles Journal, 36, 2004. “Peg Solitaire”, in Knots and Borromean Rings, Rep-Tiles and Eight Queens, Cambridge Univ. “Purging pegs properly”, in Winning Ways for Your Mathematical Plays, 2nd ed., Vol. The Ins and Outs of Peg Solitaire, Oxford Univ.


 0 kommentar(er)
0 kommentar(er)
